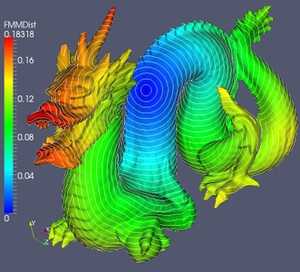
The computation of geodesic distances on a triangle mesh has many applications in geometry processing. The fast marching method provides an approximation of the true geodesic distance field. We provide VTK classes to compute geodesics on triangulated surface meshes. This includes classes for computing the geodesic distance field from a set of seeds and to compute the geodesic curve between source and destination point(s) by back-tracking along the gradient of the distance field. The fast marching toolkit (Peyre et. al.) is internally used. A variety of options are exposed to guide front propagation including the ability to specify propagation weights, constrain to a region, specify exclusion regions, and distance based termination criteria. Interpolators that plug into a contour widget, are provided to enable interactive tracing of paths on meshes.